Search engines are designed with two goals in mind:
to retrieve documents relevant to the user
and to reject the documents that are non-relevant to the users
As a criterion for the correct selection of relevant documents recall metrics could be used. This metric is defined as the minimum of the type II error - min false positive samples. In our case, it is an incorrect (false) classification of the relevant document as negative, i.e. not subject to choice.
$$Recall = \frac{TP}{TP+FN}$$
On the other hand, the precise selection of only relevant documents can be checked using another metric - precision. It is defined as a minimum of the type I error, i.e. min false negative samples. In our case, a false negative means that the document is selected when it shouldn't be.
$$Precision =\frac{TP}{TP+FP}$$
Ideally both precision and recall should be as high as possible, but depending on your use case, you may want to optimize for either precision or recall. Consider the following two use cases when deciding which approach works best for you.
Use case: Urgent documents
Say you want to create a system that can prioritize documents that are urgent from ones that are not. A false positive in this case would be a document that is not urgent, but gets marked as such. The user can dismiss them as non-urgent and move on.
A false negative in this case would be, a document that is urgent, but the system fails to flag it as such. This could cause problems!
In this case, you would want to optimize for recall. This metric measures, for all the predictions made, how much is being left out. A high recall model is likely to label marginally relevant examples. This is useful for cases where your category has scarce training data.
Use case: Spam filtering
Say you want to create a system that automatically filters email messages that are spam from messages that are not. A false negative in this case would be a spam email that does not get caught and that you see in your inbox. Usually, this is just a bit annoying.
A false positive in this case would be an email that is falsely flagged as spam and gets removed from your inbox. If the email was important, the user might be adversely affected.
In this case, you would want to optimize for precision. This metric measures, for all the predictions made, how correct they are. A high-precision model is likely to label only the most relevant examples, which is useful for cases where your category is common in the training data.
The selection method may be one of the following types: lexical, semantic, and hybrid.
Lexical (full-text) selection is usually based on creating an index of bag-of-words (BoW) found in the sentence (text), thus creating the sparse vector where each dimension in this vector corresponds to the dictionary entry of the word and the value represents the amount of this word in the sentence (text). As an example of this approach, let's consider BM25 algorithm that ranges the documents in the corpus according to their relevance to the prompt (query).
There are lots of improvements to classic BM25 algorithms. Take a review of some here.
BM25
Given the query \(Q\), containing keywords \(q_1, ..., q_N\) the BM25 score of the document \(D\) is
$$score(D, Q) = \sum_{i=1}^{n} IDF(q_{i}) \frac{f(q_i, D)(k_1+1)}{f(q_i, D)+k_1(1-b+b*\frac{\left\lvert D \right\rvert}{avgdl})}=$$
$$(k_1+1)\sum_{i=1}^{n} IDF(q_{i}) \frac{f(q_i, D)}{f(q_i, D)+k_1(1-b+b\frac{\left\lvert D \right\rvert}{avgdl})}$$
where \(k_1 \in [1.2,2]\) is a saturation external parameter (\(k_1+1\) is called boost), \(f(q_1, D)\) is the number of times that the keyword \(q_i\) occurs if the document \(D\), \(\vert D \vert\) is the length of the document in words, and \(avgdl\) is the average document length (in words) in the corpus from where the documents are drawn. \(IDF(q_i)\) is the inverse document frequency of the term \(q_i\). It is usually calculated as
$$IDF(q_i)=ln(\frac{N-n(q_i)+0.5}{n(q_i)+0.5}+1)$$
where \(N\) is the total number of documents in the corpus, \(n(q_i)\) is the number of all documents containing \(q_i\).
Let's look at using BM25 within ElasticSearch as an example.
Create an index and add several documents to it:
POST _bulk { "index" : { "_index" : "kotlin_articles", "_id" : "1" } } { "text" : "Kotlin Programming Language" } { "index" : { "_index" : "kotlin_articles", "_id" : "2" } } { "text" : "Learn Kotlin - Kotlin Free Tutorial" } { "index" : { "_index" : "kotlin_articles", "_id" : "3" } } { "text" : "Java vs. Kotlin - Part1: Performance" } { "index" : { "_index" : "kotlin_articles", "_id" : "4" } } { "text" : "Java vs. Kotlin - Part2: Bytecode" } { "index" : { "_index" : "kotlin_articles", "_id" : "5" } } { "text" : "Anything Java can do Kotlin can do better" }
The simple search with "Kotlin" query:
GET /kotlin_articles/_search
{
"query": {
"match": {
"text": "Kotlin"
}
}
}
gives the following scores:
{
"took": 1,
"timed_out": false,
"_shards": {
"total": 1,
"successful": 1,
"skipped": 0,
"failed": 0
},
"hits": {
"total": {
"value": 5,
"relation": "eq"
},
"max_score": 0.120948985,
"hits": [
{
"_index": "kotlin_articles",
"_id": "2",
"_score": 0.120948985,
"_source": {
"text": "Learn Kotlin - Kotlin Free Tutorial"
}
},
{
"_index": "kotlin_articles",
"_id": "1",
"_score": 0.10522306,
"_source": {
"text": "Kotlin Programming Language"
}
},
{
"_index": "kotlin_articles",
"_id": "3",
"_score": 0.08840232,
"_source": {
"text": "Java vs. Kotlin - Part1: Performance"
}
},
{
"_index": "kotlin_articles",
"_id": "4",
"_score": 0.08840232,
"_source": {
"text": "Java vs. Kotlin - Part2: Bytecode"
}
},
{
"_index": "kotlin_articles",
"_id": "5",
"_score": 0.07130444,
"_source": {
"text": "Anything Java can do Kotlin can do better"
}
}
]
}
}
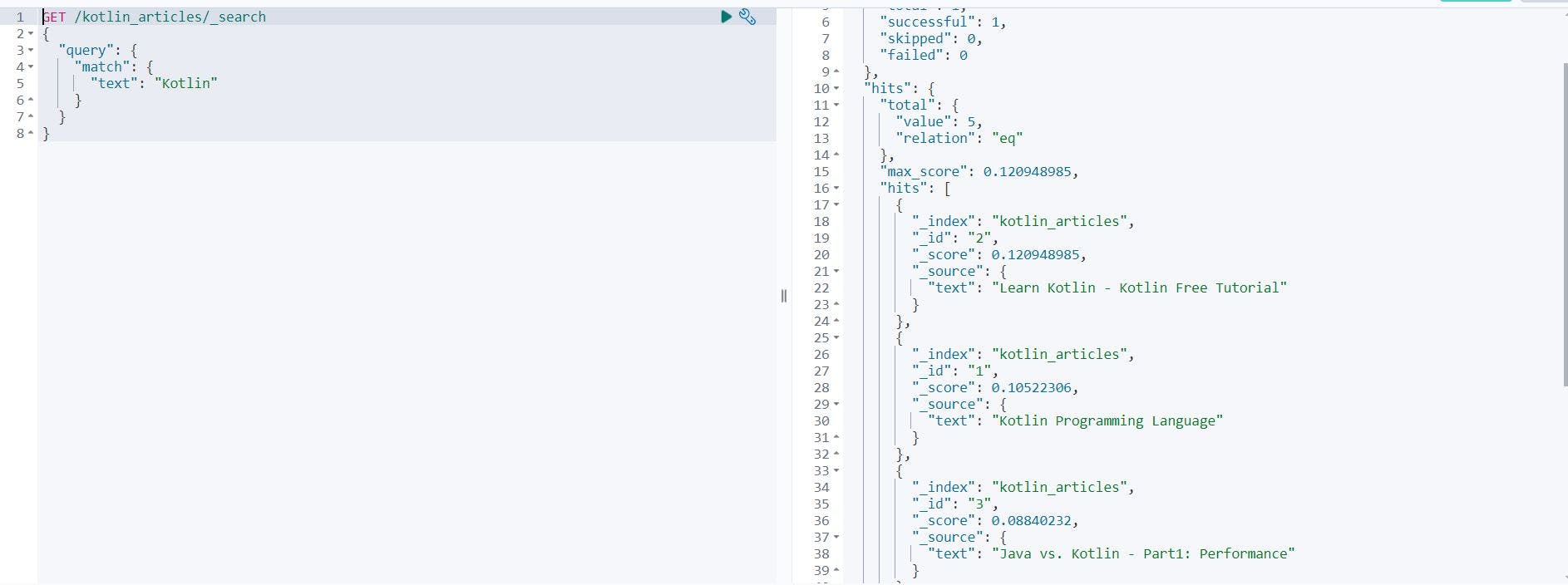
Now we can check whether the issued metric value coincides with the theoretical one. To check, let's take the most relevant document and substitute its parameters into the ranking function.
$$IDF=ln(1+\frac{(docCount - f(q)+0.5)}{f(q)+0.5})=ln(1+\frac{(5-5+0.5)}{5+0.5})=0.087$$
$$score=(k_1+1)IDF\frac{f(q, D)}{f(q, D) + k_1(1-b+b*\frac{fieldLen}{avgFieldLen}}=$$
$$(1.2+1)0.087\frac{2}{2+1.2*(1-0.75+0.75*\frac{5}{5.2})}=$$
$$2.20.087\frac{2}{2+1.2(0.25+0.750.96)}=2.20.087*\frac{2}{2+1.2*(0.25 + 0.72)}=$$
$$2.20.087\frac{2}{2+1.20.97}=2.20.087\frac{2}{3.164}=0.087*1.39=0.1209$$
To cross-check this, let’s run the calculations using the Explain API:
GET /kotlin_articles/_explain/2
{
"query": {
"match": {
"text": "Kotlin"
}
}
}
{
"_index": "kotlin_articles",
"_id": "2",
"matched": true,
"explanation": {
"value": 0.120948985,
"description": "weight(text:kotlin in 1) [PerFieldSimilarity], result of:",
"details": [
{
"value": 0.120948985,
"description": "score(freq=2.0), computed as boost * idf * tf from:",
"details": [
{
"value": 2.2,
"description": "boost",
"details": []
},
{
"value": 0.087011375,
"description": "idf, computed as log(1 + (N - n + 0.5) / (n + 0.5)) from:",
"details": [
{
"value": 5,
"description": "n, number of documents containing term",
"details": []
},
{
"value": 5,
"description": "N, total number of documents with field",
"details": []
}
]
},
{
"value": 0.63183475,
"description": "tf, computed as freq / (freq + k1 * (1 - b + b * dl / avgdl)) from:",
"details": [
{
"value": 2,
"description": "freq, occurrences of term within document",
"details": []
},
{
"value": 1.2,
"description": "k1, term saturation parameter",
"details": []
},
{
"value": 0.75,
"description": "b, length normalization parameter",
"details": []
},
{
"value": 5,
"description": "dl, length of field",
"details": []
},
{
"value": 5.2,
"description": "avgdl, average length of field",
"details": []
}
]
}
]
}
]
}
}
Note that BM25 as TF-IDF as well don't have sound theoretical properties (in contrast to Probabilistic Retrieval Model)
Read more
Understanding TF-IDF and BM-25 - KMW Technology (kmwllc.com)
Rank Product Statistic
$$RP(g) = \left(\prod_{i=1}^k r_{g,i}\right)^{\frac{1}{k}}$$
Help
Run ELK in docker:
docker network create elastic
docker pull docker.elastic.co/elasticsearch/elasticsearch:8.12.2
docker run --name elasticsearch --net elastic -p 9200:9200 -e "discovery.type=single-node" -e "xpack.security.enabled=false" -t docker.elastic.co/elasticsearch/elasticsearch:8.12.2
docker pull docker.elastic.co/kibana/kibana:8.12.2
docker run --name kibana --net elastic -p 5601:5601 docker.elastic.co/kibana/kibana:8.12.2
For a secure environment, re-create the enrollment token and password for Kibana:
docker exec -it es01 /usr/share/elasticsearch/bin/elasticsearch-reset-password -u elastic
docker exec -it es01 /usr/share/elasticsearch/bin/elasticsearch-create-enrollment-token -s kibana
or use docker-compose, create a file named: elasticsearch.yml
version: "3"
services:
elasticsearch:
image: docker.elastic.co/elasticsearch/elasticsearch:8.9.2
ports:
- 9200:9200
- 9300:9300
environment:
discovery.type: 'single-node'
xpack.security.enabled: 'false'
NEWSFEED_ENABLED: 'false'
TELEMETRY_OPTIN: 'false'
TELEMETRY_ENABLED: 'false'
SERVER_MAXPAYLOADBYTES: 4194304
KIBANA_AUTOCOMPLETETIMEOUT: 3000
KIBANA_AUTOCOMPLETETERMINATEAFTER: 2500000
kibana:
image: docker.elastic.co/kibana/kibana:8.9.2
depends_on:
- elasticsearch
ports:
- 5601:5601
and
docker compose -p elasticsearch -f elasticsearch.yml up -d

